Раздел: Документация
0 ... 22 23 24 25 26 27 28 ... 49 Принимая для оптимальной настройки MP, например, граничный апериодический процесс замкнутого контура, получаем желаемый характеристический полином АкелО>) = (Р + шб)2 = р2 + 2соб + со§. При этом базовая частота соб = т"" , относительное время пе- п.п.жел реходного процесса т„„ = 4,8, перерегулирование а = 0 %. Из условия Dip) = Dxtn(p) определяются значения параметров MP: kt =(wl+d\l2 +d2)lbi; k2 = (2соб + d\ -l2)/bi. Значение co6 находится по желаемому быстродействию /п.„.жел, ограниченному перегрузочной способностью двигателя. Для реализации MP требуется вычислитель коэффициентов кх и к2 и умножитель их на переменные х{ и х2. Современная быстродействующая микропроцессорная техника позволяет реализовать данную адаптивную систему управления, структурная схема которой приведена на рис. 5.31. Полученный самонастраивающийся модальный регулятор обеспечит в пределах перегрузочной способности двигателя заданный оптимальный динамический режим электропривода при определенном диапазоне возможных изменений двух параметров - активного сопротивления якорной цепи r и момента инерции /. Для двухконтурного электропривода, выполненного по схеме подчиненного регулирования, изменения параметров r и / нарушат оптимальную настройку как регулятора тока с передаточной функцией Wpc(p) = кРС по.тТ; knkor2Tilp о k0.rka J так и пропорционального регулятора скорости с передаточной функцией *тг 4Г Сформировав с помощью АНУ параметры r и /, можно их ввести в регуляторы соответственно тока и скорости. Адаптивное наблюдающее устройство позволяет при отмеченных выше условиях достаточно точно восстановить изменяемые параметры и переменные состояния объекта управления, а также на их основе сформулировать аналитическим способом алгоритм оптимального адаптивного управления. Однако даже для простого электропривода с характеристическим полиномом второго порядка и двумя изменяемыми параметрами адаптивная система управления оказывается весьма сложной, что наглядно видно из приведенной на рис. 5.31 схемы. Наличие нелинейностей в электроприводе в сочетании с колебательными звеньями затрудняет формирование аналитическим способом адаптивного алгоритма управления. В этом случае приближенную адаптацию можно построить не на аналитической, а на логической основе с помощью адаптивного фаззи-наблюдателя (АФН). Рассмотрим вариант электропривода с одним изменяемым параметром - моментом инерции /=/0 +Д/, где Д/=уаг. Если создан наблюдатель для подвижной части электропривода без учета изменений /, то производная ошибки наблюдателя оценивается величиной ~ . Д/ М ДС0у = со - со = --- -. у/0 + Д/ /0 При Д/=0 ошибка наблюдателя и ее производная равны нулю, а при Д/-> оо и М= const ДсЬу -» M/JQ. Если /= const и присутствует изменяемый момент нагрузки Мнш, то производная ошибки наблюдателя оценивается величиной М лтл няг ДсЬ„ /п При Мнаг = 0 Дсо = 0, а при нарастании Мтт растет и Дюм. Из сопоставления величин Дсоу и ДсЬм следует схожесть на качественном уровне влияния изменения параметров / и Mmr в некотором диапазоне на различие в скоростях электропривода и наблюдателя его силовой части. Количественно величины Дсоу и Дсом отличаются только из-за различного характера их зависимости от изменяемого параметра - для Дсоу данная зависимость нелинейна, а для Дсом - линейна. Это позволяет для электропривода с изменяемым моментом инерции использовать приближенную сигнальную адаптацию на основе адаптивного фаззи-наблюдателя (АФН) (рис. 5.32). Фаззи-регулятор ФР формирует дополнительный управляющий сигнал им, подаваемый на вход контура момента и оказывающий компенсирующее действие на изменение момента инерции. Алгоритм ФР составляется на логической основе как функция ии двух входных переменных Дсо и Дсо, например, с пятью уровнями (NB, NS, Z, PS, РВ) и представляется в виде таблицы (см. гл. 4). Таблица отражает свод соответствующих данной зависимости правил: ЕСЛИ Дсо = РВ И Дсо = PS, ТО им = РВ; ЕСЛИ Дсо = PS И Дсо = NB, ТО иК = Z и т.д. Необходимую для оптимизации динамического режима электропривода нелинейность алгоритма ФР получают подбором зна- <-РС м
«тг «тг ФР Рис. 5.32. Структурная схема АСЭМ с фаззи-регулятором со, рад/с 180 160 140 120 100 80 60 40 20 0 -20
о 0,5 11,5 а /.А 20 10 0 -10 -20 -30 -40 о 0,5 2,5 /, с 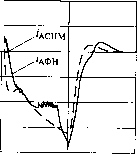 2,5 /,с 11,52 б Рис. 5.33. Диаграммы изменения скорости (я) и тока (б) при позиционировании электропривода чений центров функций принадлежности входных и выходной переменных ФР. На рис. 5.33 приведен результат моделирования отработки заданной тахограммы позиционирования электроприводом с параметрами из примера синтеза регуляторов тока и скорости (см. подразд. 5.3.2). Момент инерции электропривода в этом режиме увеличивался в 3 раза. Вариант 1 системы адаптивного управления - АСНМ согласно схеме рис. 5.31 с аналитическим алгоритмом управления - рассчитан по приведенному выше математическому описанию (кривые соАСНМ, /Аснм); вариант 2 - АСНМ с адаптивным фаззи-наблюдателем согласно схеме рис. 5.32 с логическим алгоритмом управления, составленным без помощи математического описания (кривые соАФН, /афн)- Сопоставление графиков показывает, что вариант 2, уступая незначительно по качеству отработки заданной тахограммы (кривая со3), оказывается более простым по структуре адаптивного управления и по алгоритму управления. Данный пример свидетельствует, что в задачах адаптивного управления электропривода сопоставимы и конкурентоспособны системы, построенные как на аналитической основе, так и на приближенной логической основе, т.е. на основе фаззи-логики. Контрольные вопросы 1.В каком из двух случаев: 1) Мс] = 0, Мс2 = Мтг; 2) Mci = Мс2 = - Мтг - жесткость механической характеристики будет больше для электропривода, замкнутого по вектору состояния X(t) = [е, СО] М]2 со2]г? 2.Как изменится жесткость механической характеристики электропривода с упругим механическим звеном, замкнутого по вектору состо- di da,dco2 яния X(t) dt dtdt если уменьшить вдвое время пе- реходного процесса изменением настройки модального регулятора? 3.Как отразится на наблюдателе двухмассовой подвижной части электропривода увеличение момента инерции рабочего органа /2? 4.Как изменится электромеханическая характеристика электропривода с токовой отсечкой, если систему управления дополнить отрицательной связью по скорости с коэффициентом усиления кос = 3 при неизменном задающем напряжении? 5.Какой показатель замкнутого контура принимается для настройки на так называемый модульный, или технический, оптимум? Почему этот оптимум имеет такое название? 6.В чем отличие симметричного оптимума контура скорости от модульного оптимума? 7.Поясните назначение задающего устройства и блока ограничения выходного напряжения регулятора скорости. Как меняются статические и динамические характеристики электропривода при изменении характеристик указанных элементов схемы управления? 8.Какой системе управления - с модальным регулятором или с подчиненным регулированием - вы отдали бы предпочтение, чтобы получить заданное быстродействие и демпфирование скорости рабочего органа электропривода с упругим механическим звеном? 9.В схеме на рис. 5.16 с ПИ-регуляторами тока и скорости вдвое уменьшили коэффициент обратной связи по скорости. Как при этом изменятся статические характеристики электропривода? Как это повлияет на динамические свойства контуров тока и скорости? 10.В силовой цепи питания тиристорного преобразователя произошло уменьшение напряжения на 10%. Как качественно изменятся статические и динамические характеристики контуров тока и скорости электропривода в схеме на рис. 5.16 с ПИ-регуляторами тока и скорости? 11.Какие достоинства и недостатки вы отметили бы в системе каскадного управления скоростью электропривода по принципу подчиненного регулирования координат? 12.Приведите примеры технологических установок, в которых целесообразно применение электропривода с двухзонным регулированием скорости. 13.Поясните назначение контуров регулирования тока возбуждения и ЭДС двигателя в системах двухзонного регулирования скорости. 14.Как магнитный поток двигателя влияет на его механические и электромагнитные постоянные времени? 15.Поясните назначение блоков ограничения задания тока возбуждения и выделения модуля ЭДС двигателя в схеме на рис. 5.23. Как они влияют на статические и динамические характеристики электропривода? 16.В схеме на рис. 5.23 с ПИ-регуляторами тока якоря и возбуждения, скорости и И-регулятором ЭДС двигателя вдвое уменьшили коэффициент обратной связи по скорости. Как при этом изменятся статические характеристики электропривода? Как это повлияет на динамические свойства контуров регулирования тока якоря, тока возбуждения, скорости и ЭДС двигателя? 17.При каких условиях работы электропривода возникает потребность в его адаптивном управлении? 18.Для какой задачи управления двухконтурного электропривода вы предложили бы систему с эталонной моделью с сигнальной адаптацией? 19.Какую систему адаптивного управления из рассмотренных в данной главе вы предложили бы использовать для электропривода с упругим механическим звеном и с изменяемыми моментом нагрузки и моментом инерции рабочего органа? СИСТЕМЫ УПРАВЛЕНИЯ СКОРОСТЬЮ ЭЛЕКТРОПРИВОДОВ ПЕРЕМЕННОГО ТОКА 6.1. Управление синхронным двигателем в схеме вентильного двигателя Синхронные двигатели большой мощности находят достаточно широкое применение в нерегулируемых электроприводах с длительным режимом работы благодаря своим хорошим энергетическим показателям и, в первую очередь, высокому коэффициенту мощности. Работая в двигательном режиме, данная электрическая машина может одновременно быть и генератором реактивной энергии, улучшая тем самым коэффициент мощности участка сети с асинхронной нагрузкой. Релейно-контакторная система управления синхронным двигателем, рассмотренная в гл. 2, позволяет осуществить автоматизацию процесса пуска, обеспечивает требуемые защитные функции. При необходимости регулирования скорости синхронного двигателя может быть применен, как и для асинхронных двигателей, управляемый преобразователь частоты. Наряду с традиционным частотным управлением, когда двигатель получает питание от инвертора с независимым заданием частоты, находит весьма широкое применение управление, зависимое от вращения ротора, когда частота выходного напряжения (или тока) инвертора задается частотой вращения ротора с помощью датчика положения ротора. Синхронный двигатель с таким инвертором представляет собой обращенный двигатель постоянного тока, в котором неподвижный статор является якорем, а вращающийся ротор - источником магнитного поля. Двигатель при данной схеме включения называется вентильным двигателем (ВД). Синхронные двигатели малой мощности с сильными постоянными магнитами используются преимущественно в регулируемом электроприводе по схеме ВД. По сравнению с коллекторными двигателями постоянного тока они обладают лучшими динамическими, габаритными и стоимостными показателями. 6.1.1. Вентильный двигатель Простота управления двигателем постоянного тока обусловливала до недавнего времени его преимущественное применение в регулируемом электроприводе. Слабым звеном в этом приводе является сам двигатель, дорогой в изготовлении из-за сложности 0 ... 22 23 24 25 26 27 28 ... 49 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












