Раздел: Документация
0 ... 40 41 42 43 44 45 46 ... 49 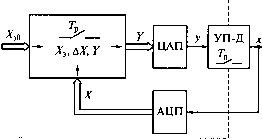 Рис. 8.3. Схема цифрового контура электропривода с микроЭВМ выпрямитель с тиристорными или транзисторными ключами, широтно-импульсный преобразователь). При этом в ЦСУ будут действовать два временных квантователя в общем случае с разными периодами Тр и Тп. Квантователи, условно изображенные на рис. 8.3 ключами, вращающимися с угловыми частотами 2к/Тр и 2к/Ти, обновляют значения управляющего воздействия у на выходе микроЭВМ и ЭДС УП в моменты замкнутого состояния ключей. Работа квантователей, т.е. работа микроЭВМ и УП должна быть синхронизирована. Если значения периодов Тр и Ти кратны одно другому и между передними фронтами начальных импульсов отсутствует временной сдвиг Ат, то вместо двух последовательно действующих квантователей можно рассматривать один с периодом Г=тах(7р, Тп).(8.13) В процессе работы ЦСУ при сохранении синхронизма синфаз-ность действия квантователей по ряду причин может нарушаться, вызывая дополнительное чистое запаздывание Ат0, изменяемое в пределах 0<Ax0<min(7;p, Та).(8.14) При Тр= Тп Ат0тах= Т. Так как надежную информацию о конкретном значении и изменении Ат0 получить затруднительно, то в практических расчетах по синтезу и анализу ЦСУ электропривода принимают в зависимости от конкретной задачи одно из двух значений чистого запаздывания - Дт0 = О или Ат0 = Т [12, 24]. Согласно теории автоматического управления (ТАУ) ЦСУ с программным способом управления без учета квантованности по уровню математически описываются на основе теории импульсных систем. Непрерывный сигнал x(t) преобразуется в квантованный по времени импульсный сигнал хп(пТ) с амплитудно-импульсной модуляцией при Ти = const, когда амплитуда импульса равна или пропорциональна мгновенному значению x(t) в начале каждого периода дискретности Г (рис. 8.4). При Тн>0 им- л хн(пТ) О Т IT ЪТ ATnTt Рис. 8.4. Непрерывный и квантованный по времени сигналы ЦСУ пульсный сигнал вырождается в так называемую решетчатую функцию х[пТ] = х[п], целочисленный аргумент которой определяется номером такта п временной дискретности. Анализ и синтез импульсных систем основаны на дискретном преобразовании Лапласа в формах [24]: D-преобразования D(p) = 2Zf[nT\e-pnT л=0 или преобразования (8.15) (8.16) ад = I/Mr". Здесь ДпТ] - решетчатая функция (оригинал), f[nТ] = /[«]; Dip) и F(z) - изображения решетчатой функции; z = epT- На рис. 8.5 приведена структурная схема, используемая в ТАУ для математического описания преобразования непрерывного сигнала в дискретный по времени. Импульсный элемент (ИЭ) представляется в схеме дельта-функцией 8(t- nТ) = оо для t=nT, 5(г-лГ) = 0 для t* nT с изображением по Лапласу выходного сигнала ИЭ со ХЪ(Р) = \x(t)b(t-nT)-PTdt = х[п]. Передаточная функция экстраполятора определяется отношением изображений его выходной и входной величин при n = const:
1 Рис. 8.5. Структурная схема импульсного звена совместно с непрерывным звеном W3(p) = = ?tM = Xl(p).(8.17) Xs(p) x[n] Следовательно, прямоугольной форме импульса с продолжительностью, равной Т, на выходе экстраполятора нулевого порядка x3(t) = l(t)-l(t-T) соответствует изображение 1 е~рТ 1 - е~Рт р р р равное передаточной функции экстраполятора, т.е. К(Р) = }~Л- = -•(8.18) Р zp Экстраполятор совместно с непрерывным звеном (НЗ) составляют приведенное звено (ПЗ) с приведенной передаточной функцией (ППФ) Wu(P) = W3(pWm(p) = Z~lW™(p).(8.19) Z Р Последний элемент в структурной схеме на рис. 8.5 означает выделение из временной реакции НЗ или ПЗ на импульсное воздействие значений y(t) в дискретные моменты времени, т. е. выделение решетчатой функции у[п]. Дискретную передаточную функцию (ДПФ) для приведенного звена можно найти как z-преобразование выражения (8.19): Wn(z) = Z JizI *Ш<£>} = iz!Z&(£>l(8.20) Z Pi Z VP Так как l/р есть Лапласово изображение единичной функции 1(f), то WH3(p)/p представляет собой изображение переходной функции h(t) непрерывного звена, т.е. реакции НЗ на единичный скачок. Следовательно, Zj**"3 = Z{hm[n\) и Wn(z) = -Z{hm[n]},(8.21) где hH3 [п] - переходная решетчатая функция НЗ. Используя полученные структурную схему для звеньев с импульсным входным воздействием и их передаточные функции, можно составить структурную схему и ДПФ для цифрового контура регулирования координаты электропривода с учетом квантования по времени. Приведенная на рис. 8.6, а структурная схема не учитывает нелинейность от квантованное™ по уровню. Непре- хМ) АЦП 1 хЛп] Ицр(г) ас [л] 1 1 (z-DKzp) ЦАП АЦП y(t)
Рис. 8.6. Развернутая (а) и свернутая (б) структурные схемы цифрового контура регулирования рывным звеном в данной схеме является объект управления с передаточной функцией Woy(p), выходной координатой у которого может быть, например, ток или момент, скорость, положение (угол поворота) электропривода. К ПЗ целесообразно отнести все звенья разомкнутого в точке Р контура с непрерывной передаточной функцией WAP) = *цап*о*ацп(8-22) и дискретной Wn{z) АцапсЛацп Z{hoy[n}}, (8.23) где ка - коэффициент обратной связи. ДПФ разомкнутого контура Wu(z)=Ww(z)WTi{z),(8.24) где Wup(z) - ДПФ цифрового регулятора. В свернутом виде структурная схема цифрового контура регулирования показана на рис. 8.6, б. Для определения динамических свойств цифрового контура регулирования решают задачу анализа, т.е. рассчитывают переходную функцию замкнутого контура х[п] = h[n] для х3[п] = 1[п], по которой оценивают перерегулирование и время переходного процесса. Процесс может быть рассчитан на основании ДПФ замкнутого контура X(z) W,(z) B{z) W{z) = X3(z) l + W0(z) D(z) (8.25) 265 с помощью формулы разложения. Однако для получения общего решения для х[п] требуется определение корней характеристического полинома D(z), что в случае высокого порядка полинома оказывается непростой задачей. Без определения корней расчет переходного процесса выполняют численно методом разностных уравнений. Для ДПФ замкнутого контура W(Z} = boZm +b\zmx + ... + bm xz + bm = X(z) щ d0z +d]z~[ + ... + d, lz + d, X3(zY где / > m, после деления числителя и знаменателя на z с учетом теоремы запаздывания можно составить соответствующее (8.26) разностное уравнение dQx[n] + djX[n -1] +... + dix[n - /] =27) bQx3[n -(/ -m)] + bxx3\n - (I - m + 1)] +... + bmx3[n - I). Решая (8.27) относительно искомой функции х[п], получим рекуррентную формулу, по которой последовательно рассчитываются значения функции х[п] на каждом такте по значениям входной переменной х3 на данном такте и по значениям х3 и х на предыдущем такте. 8.4. Методика синтеза цифрового контура Цель синтеза - определить тип и параметры цифрового регулятора, обеспечивающего желаемые статические и динамические показатели электропривода. К желаемым показателям так же, как и для аналогового контура, могут относиться точность регулирования координаты, время переходного процесса, перерегулирование. Если при синтезе достигается наилучшее значение какого-либо показателя (минимальное время переходного процесса, максимальная точность регулирования и т.п.), то такой синтез будет оптимальным по данному показателю, а процедура его выполнения - оптимизацией контура по данному показателю. Цифровой контур в свернутом виде (см. рис. 8.6, б) состоит из двух звеньев: цифрового регулятора (ЦР) - изменяемой части и приведенного непрерывного звена - неизменной части. Поэтому непосредственным объектом синтеза является ЦР. Метод синтеза последовательной коррекции по желаемой передаточной функции разомкнутого контура, используемый для непрерывных СУЭП, применим и для цифровых систем управления, для которых вместо непрерывных передаточных функций должны использоваться ДПФ. Условие определения ДПФ ЦР: Wn(z) Здесь W (z) " жел WnP(z) = Ж!ГЛ!} (8-28) желаемая ДПФ разомкнутого контура; Ma) = -y--(8.30) желаемая ДПФ замкнутого контура, где DXCI1(z) - желаемый дискретный характеристический полином (ДХП) замкнутого контура. Процедура синтеза ЦР выполняется следующим образом. Пусть заданы динамические показатели в виде желаемой непрерывной переходной функции замкнутого контура /гжел(0- Эта функция при заданном периоде квантования Т переводится в решетчатую - /гжел[«]. Желаемая ДПФ замкнутого контура находится согласно выражению (8.21): жел(0 == -Z{hMm[n]}.(8.31) X3(z) z По формуле (8.29) определяется rV0xen(z), а по формуле (8.28) с учетом (8.23) - ДПФ цифрового регулятора „г , ч Ожел() Z(ft»„M) (8.32) 7 - 1 (1 - -y Z{Лжел[n]})Z {hoy [fi]}цапАЦПо В данном синтезе остается вопрос, можно ли реализовать выбранную желаемую динамику при заданном объекте управления? Ведь пожелать можно любую динамику, например, сколь угодно быструю. Можно ли ее реализовать в замкнутом цифровом контуре теоретически и практически? Ответ на данный вопрос дают условия реализуемости желаемой динамики цифрового контура регулирования [19]. Пусть ДПФ ПЗ имеет следующий вид: Wn(z) =---.(8-33) где P(z), Q{z) - полиномы порядка соответственно 1Р и /е; vn - порядок астатизма ПЗ. Для принятых ДПФ ПЗ (8.33) и замкнутого контура (8.25) составим условия реализуемости. 0 ... 40 41 42 43 44 45 46 ... 49 |
||||||||||||||||||||||||||||||||||












