Раздел: Документация
0 ... 41 42 43 44 45 46 47 ... 49 1.Условие физической реализуемости: желаемая ДПФ замкнутого контура (8.30) должна быть правильной дробью, в которой порядок числителя т меньше порядка знаменателя /; если в Wu{z) есть запаздывание (е~рт), то оно должно быть также в Wxai(z)- 2.Условие «грубости» системы: небольшие изменения параметров ЦР могут вызывать незначительные изменения показателей процесса в замкнутом контуре. Приближенно это означает, что процентное изменение показателя процесса не должно превосходить процентное изменение параметра. Для выполнения этого условия требуется, чтобы ПЗ было устойчивым и минимально фазовым, т.е. полиномы P(z) и Q(z) не должны иметь правых (положительных) нулей. 3.Условие получения желаемого процесса в любые моменты времени t = (п + г) Т, где s = < 1, внутри периода дискретности Т: WMin{z) должна иметь в составе B(z) все нули полинома P(z), что может быть достигнуто представлением В(z) в форме произведения полиномов P(z) и M(z), т.е. W(Z) = -P{Z)M{Z\(8.34) Акел(г) Акел(г) где M(z) - полином порядка lM = m - 1Р, подлежащий определению. 4.Условие получения в контуре регулирования астатизма порядка v: l-Wm(z) = iz~iy"lz),(8.35) Акел(г) где N(z) - полином порядка lN=l-v, подлежащий определению. Если выполнить условия в отношении полиномов ДПФ и объединить выражения (8.34) и (8.35), то можно получить результирующее уравнение реализуемости P(z)M(z) + (z- \)vN(z) = Дел(г),(8.36) в котором lP+ lM< I, V + lN= I. По данному уравнению могут быть найдены методом сравнения коэффициентов правой и левой частей полиномы M(z) и N(z). Следовательно, могут быть определены ДПФ: w,m{z)= P(zW{z) ;(8.37) W„(z) (z-\y-v"N(z) Таким образом, уравнение реализуемости (8.36) позволяет выполнить корректный синтез цифрового контура, обеспечива- ющего желаемую динамику при выполнении перечисленных выше условий. В данном синтезе используется известная для непрерывных систем методика стандартных уравнений. По желаемым значениям динамических показателей выбирается соответствующее стандартное характеристическое уравнение Dxe,,(p), которое переводится в дискретную форму 7)жел(г), имеющую тот же порядок /= v + lN. Найденные из уравнения реализуемости полиномы M(z) и N(z) позволяют определить по формуле (8.38) тип и параметры цифрового регулятора. Рассмотрим частный случай ДПФ замкнутого контура, когда W(z) = = B(z)z-=hz-«-m)++ ... + bmz~l. (8.39) z Выходная координата данного замкнутого контура согласно выражению (8.27) х[п] = Ьах3[п - (/- т)] + Ьхх3[п - (/ -т + \)} + ... + Ьтх3[п -/]. (8.40) Если на вход замкнутого контура подать единичный входной сигнал х3[п] = \ [п], то переходный процесс в соответствии с (8.40) завершится за конечное число тактов п = I, после которых х[п] = х3[п] = Ь0 + Ьх +... + bm = const = 1. Таким образом, обеспечение желаемой ДПФ замкнутого контура в форме (8.39) является условием оптимальности контура по быстродействию, т.е. условием минимального времени переходного процесса >n.nmin = /T,(8.41) где / - порядок характеристического полинома. 8.5. Оптимизация цифрового контура тока электропривода с тиристорным преобразователем Задачей оптимизации данного контура регулирования является синтез цифрового регулятора тока (ЦРТ) по выбранному условию оптимизации, т.е. определение типа и параметров ЦРТ, обеспечивающего оптимальные динамические показатели контура тока. За такие показатели обычно принимают минимальные перерегулирование и время переходного процесса. При выполнении синтеза используем следующие допущения: режим непрерывного тока для тиристорного преобразователя (ТП); динамика контура тока «в малом», т.е. при малом диапазоне изменения угла открывания ТП Да; дискретная расчетная динамическая модель ТП с усреднением ЭДС на интервале проводимости Ти. Тиристорный преобразователь в динамических режимах представляет собой весьма сложную нелинейную импульсную систему с изменяющимся интервалом дискретности (рис. 8.7) Левиту 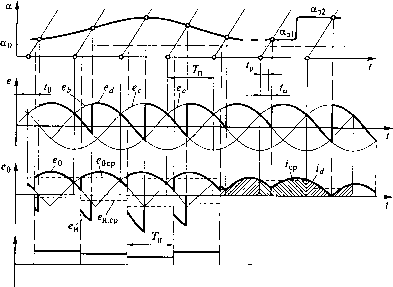 ОТп 2ТП ЗГП 4ГП t Рис. 8.7. Диаграмма формирования ЭДС ТП как дискретного звена Т = (Тп + (а2 - а,)) 2я/с (8.42) где Тп - интервал проводимости в установившемся режиме, с; аь сх2 - углы открывания тиристоров соответственно на данном и последующем интервалах проводимости, рад;/с - частота питающей сети, Гц. При этом Тп=~,(8.43) где m - пульсность ТП, равная числу фаз в нулевых схемах и удвоенному числу фаз в мостовых схемах. При возрастании а величина Г увеличивается, а при снижении а - уменьшается. Однако при замене реальной выпрямленной ЭДС преобразователя ed(t) на усредненные на интервалах Тп величины edcp можно представить ТП линейным импульсным звеном с переменной е0 с неизменным периодом дискретности Т = Ти [25]. Сформированный таким образом импульс еи[пТп] вносит в динамике некоторую неточность Aedcp, которая тем меньше, чем меньше диапазон изменения угла открывания а. В установившемся режиме AeJcp = 0. Принимая прямоугольные импульсы edcp = eu[nTn] с неизменным интервалом дискретности Т„ за выходную ЭДС, можно пред- Да
Рис. 8.8. Структурная схема ТП как дискретного звена в режиме непрерывного тока ставить ТП импульсным линейным звеном с экстраполятором нулевого порядка (рис. 8.8). Передаточная функция такого звена для малых отклонении и с выходной переменной АУ = •---, К где В.я - суммарное сопротивление якорной цепи, Ом, имеет вид WAp) = kJ-- = ka.(8.44) ДарZP Здесь кат = - sin а - передаточный коэффициент ТП по К току, А/рад; Ud0 - среднее значение выпрямленного напряжения при а = 0, В. Кроме дискретности ТП в контуре тока имеет место дискретность цифровой системы управления (ЦСУ) - Тр. Работа ЦСУ синхронизируется с питающей ТП сетью, что означает синхронизацию двух периодов квантования Тр и Тп относительно фиксированной точки напряжения питания, обычно относительно точки естественного открывания ТП. Если требуемое для измерения тока и расчета алгоритма управления значение Тр меньше Ти, то за результирующую дискретность цифрового контура тока принимают период дискретности ТП. Обычно измеряемой величиной тока является его среднее значение idna интервале Тп, подаваемое в микроЭВМ в момент естественного открывания ТП (см. рис. 8.7). Если время tp = Тр < ta = --, то отработка изменения задающе- го угла происходит без дополнительного запаздывания на величи- сх ну Т„ (изменение а от аз1 до аз2 на рис. 8.7). Если же tp > -г-г, то 2л/с возникает запаздывание открывания ТП с новым значением а на величину Т„. Для исключения такого запаздывания используют специальную компенсирующую коррекцию [23]. Структурная схема цифрового контура тока без учета ЭДС двигателя представлена на рис. 8.9. За входную переменную контура тока принято приращение угла открывания ТП Дсхзт, которое задает требуемое изменение тока, а за выходную переменную - приращение среднего за период Ти тока А/ или соответствующая ему величина сигнала обратной связи по току, выраженная через угол открывания ТП, Да3.т 1 Аазт [л] IVpjiz) 1 iz-DKzp) д/ 1/(7яР+1) Да 0 т [л] 1 Д«ол сацп Д"о.т -о.т Рис. 8.9. Структурная схема цифрового контура тока Аа0.т = ацгА.тЛ = А;ТД/, где к01 - передаточный коэффициент датчика тока, В/А; кАПП - передаточный коэффициент АЦП, В-1 (кАт = Аи 10). Цель оптимизации контура - определить тип и параметры цифрового регулятора тока, т.е. определить его ДПФ Wvl{z). Воспользуемся рассмотренной в подразд. 8.4 методикой синтеза с расчетными формулами (8.28) и (8.29). Согласно структурной схеме передаточная функция приведенного непрерывного звена (ПНЗ) Wn{p) = learK,Z~l * n,(8-45) z р(Тяр + \) где Тя - электромагнитная постоянная времени якорной цепи ТП-Д, с. В соответствии с формулой (8.23) ДПФ ПНЗ Wn(z) = kmK*-z\ 1 } = *eT*.T lz{h[n]}. (8.46) z {р(Тяр + \)\z Здесь h[n] - решетчатая переходная функция непрерывного звена; т -п- h[n] = 1 - е т«, где Т - интервал дискретности по времени, с, равный Тп. Из таблицы для изображений решетчатых функций [13] Z{h[n]}= ~dz(8.47) где йя = e"r/r». Тогда Wn{z) = kmK,--(8.48) За желаемый переходный процесс контура тока принимаем экспоненциальный закон с параметром Тт для модульного оптимума: 272 Д/жел = Д/П-е7),(8.49) где Тт = 27;, Т„ = Тп- Выражению (8.49) соответствует решетчатая функция -пТ Да0.т[я] = Да3.т(1-е Гт ), откуда Д«з.т Так как желаемая ДПФ замкнутого контура Wxejl(z) = - Z{Ktli Щ = -Ь,(8.50) ZZ-dT ~т где dT = е Гт, то ДПФ разомкнутого контура согласно (8.29) ожел(г) = 4.(8.51) z-l В соответствии с (8.28), (8.44) и (8.51) ДПФ регулятора тока: Wn(z) kKAl-dJ z-l ЦРТ z-l Итак, с учетом принятых для оптимизации цифрового контура тока допущений получен цифровой регулятор тока (ЦРТ) с ДПФ, соответствующей цифровому ПИ-регулятору. Пропорциональная часть ЦРТ определяется коэффициентом кц?т =--= ЬА .(8.53) катк0.т(1 ~ dx) 1 - йя кпкот Интегральная часть ЦРТ, равная *црт(1-4.) Z-1 (8.54) имеет знаменатель, обращающийся в ноль при z = 1 (р = 0). Сравним параметры аналогового и цифрового регуляторов тока при настройке на модульный оптимум. Для аналогового ПИ-РТ Ил-Ы-гт*--1-J R* =рт+ - ,(8.55) Т к к Т п к кТ п где ТТ = 2ТЦ. Для цифрового ПИ-РТ при Т -> 0 пропорциональная часть согласно (8.53) 10 Терехо»273 0 ... 41 42 43 44 45 46 47 ... 49 |












