Раздел: Документация
0 ... 39 40 41 42 43 44 45 ... 49 Глава 8 ЦИФРОВЫЕ СИСТЕМЫ УПРАВЛЕНИЯ СКОРОСТЬЮ И ПОЛОЖЕНИЕМ ЭЛЕКТРОПРИВОДА 8.1. Понятие цифровых СУЭП К цифровым системам управления (ЦСУ) относятся системы, состоящие из цифровых элементов. Термин «цифровой элемент» (ЦЭ) означает определенную конструктивную электротехническую единицу дискретного действия, выполняющую различные функции - логические, вычислительные, преобразовательные, запоминания сигналов. В составе ЦСУ цифровые элементы образуют узлы, выполняющие те или иные задачи управления. На рис. 8.1 приведена схема ЦСУ некоторой координатой х электропривода, где ЦЗУ - цифровое задающее устройство, ЦС - цифровой сумматор, ЦР - цифровой регулятор, ЦАП - цифроаналоговый преобразователь, АЦП - аналогово-цифровой преобразователь, УП-Д - система управляемый преобразователь-двигатель, в которой УП является выходной исполнительной частью СУЭП. Заглавными латинскими буквами обозначены многоразрядные цифровые сигналы. Входной цифровой сигнал хз0 устанавливает исходные парамет- ры для х3, например, хзп что означает для выход- ной управляемой координаты электропривода х, например, для перемещения, соответственно заданные значения перемещения, максимально допустимых скорости и ускорения. Данная схема ЦСУ по своей структуре аналогична непрерывной СУЭП с теми же функциональными узлами, кроме ЦАП и АЦП, но выполненными на аналоговых элементах. Достоинства ЦЗУ Аппаратная или программная часть ЦС ах ЦР X Аппаратная часть ЦАП АЦП УП-Д Рис. 8.1. Схема цифровой системы управления одной координатой электропривода ЦСУ определяются достоинствами цифровых элементов по сравнению с аналоговыми - большими помехоустойчивостью и точностью датчиков скорости и положения, простотой и удобством цифрового задания программы на движения электропривода, неуклонной тенденцией к снижению габаритов и стоимости ЦЭ, к повышению надежности и степени интеграции цифровых узлов. Функциональные узлы ЦСУ, показанные на рис. 8.1, могут быть реализованы двояко: аппаратно - каждый функциональный узел представляет собой самостоятельный отдельный блок в составе ЦСУ, выполненный на микросхемах малой и средней степени интеграции; программно - функциональные узлы выполняются на едином универсальном цифровом устройстве - микроЭВМ и алгоритм их функционирования определяется программой работы этого устройства. Для изменения алгоритма управления ЦСУ при аппаратном способе требуется замена и соответствующих блоков управления. При программном способе для изменения алгоритма управления требуется лишь изменение программы на той же элементной базе. Такие ЦСУ находят широкое применение в электроприводах производств, где возможны изменения технологических процессов, следовательно, требуются изменения и в задачах управления верхнего уровня. Благодаря быстрому совершенствованию современной технологии изготовления микроЭВМ и микропроцессорных устройств, повышению их качества и снижению стоимости программный способ управления как верхнего, так и нижнего уровней все шире внедряется в системы управления электроприводов. Цифровые СУЭП (ЦСУЭП) отличаются от непрерывных СУЭП, главным образом, элементной базой, ее дискретностью по уровню сигналов и по времени их действия. ЦСУЭП, как и непрерывные СУЭП, формируют те же требуемые задачами управления алгоритмы, используют те же методы управления - модального управления, подчиненного регулирования, последовательной и параллельной коррекции и т.п. Однако в реализации алгоритмов управления может проявляться дискретность ЦСУЭП, отражающаяся на динамических и точностных показателях электропривода. Поэтому в задачу данной главы входит рассмотрение способов учета дискретно-стей ЦСУЭП при синтезе цифровых регуляторов и оптимизации контуров регулирования координат электропривода. 8.2. Расчетные модели ЦСУ с учетом дискретности по уровню При любом способе построения ЦСУ дискретное представление значений цифровых переменных, определяемое конечным числом их разрядов, вносит отличие в преобразование сигнала по сравнению с непрерывными СУЭП. Эта так называемая дискретность по уровню, или квантовость по уровню, может оказывать существенное влияние на динамические и точностные показатели электропривода с ЦСУ. Поэтому целесообразно оценить влияние данной дискретности на преобразование сигнала в цифровом элементе. Наибольшая квантованность сигнала имеет место в таких преобразовательных элементах, как цифровые датчики, представляющие собой аналогово-цифровые преобразователи (АЦП) и цифроаналоговые преобразователи (ЦАП). Рассмотрим АЦП. Квантованность по уровню выражается в его многоступенчатой характеристике управления (рис. 8.2, а). Такая характеристика вносит нелинейность в ЦСУ. Передаточный коэффициент АЦП, представляющий собой отношение единицы выходной величины (1) к единице входной величины (Axq) - Wt =~r- = W,(8-1) Дх0 определяет только усредненную выходную переменную УсР = £Ацп*-(8.2) Если заменить выходную переменную у на переменную х в масштабе входной величины х, то разность х-х = Дхп(8.3) 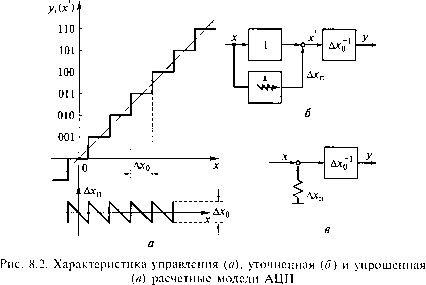 определит помеху от квантованности по уровню в виде периодической функции от х. Тогда описание нелинейной характеристики АЦП будет определяться выражениями У = AXqx; х = х + Ахп; Дхп=£дхп/;(8.4) Дхш = -(х - /Ах0), при (/" - 0,5)Ах0 < х < (/ + 0,5)Дх0 иначе Дхп/ = О, которым соответствует расчетная модель АЦП, приведенная на рис. 8.2, б. Средний квадрат ошибки от квантования будет определяться как дисперсия помехи Дхп2=- J {-х)Чх = -.(8.5) 0 -0,5ДХ„11 При интегральной оценке влияния помехи квантования расчетная модель АЦП упрощается (рис. 8.2, в). Преобразователь представляется линейным звеном, на входе которого кроме полезного сигнала х действует помеха Ахп типа «белого шума» с равновероятными значениями в пределах -0,5Дх0... 0,5Дх0 с корреляционной функцией Лп(х) = Ахп25(0,(8.6) где 5(/) - дельта-функция, и спектральной плотностью, равной дисперсии помехи: W = Ax2=.(8.7) В таком представлении АЦП влияние помехи от квантования сигнала можно учесть интегральной оценкой ошибки регулирования Дх координаты электропривода Дх2 = - Пи/п(усо)25п(соУсо = l\Wn(M)\2dc», (8.8) л о1271 о где Wn(yco) - модуль передаточной функции системы регулиро- х вания по каналу помехи квантования, равный Ахп Если при описании АЦП ограничиться усредненной характеристикой управления (8.2), то эффект квантования не будет учитываться в преобразовании сигнала в АЦП. Таким образом, имеются три варианта расчетной модели АЦП с квантованным по уровню выходным сигналом: модель 1 - нелинейное звено с многоступенчатой релейной характеристикой управления (см. рис. 8.2, а), характеризуемой структурной схемой, показанной на рис. 8.2, б; модель 2 - линейное звено с дополнительным сигналом в виде помехи, имеющей вероятностный характер типа «белого шума» с постоянной спектральной плотностью, равной дисперсии помехи (см. рис. 8.2, в); модель 3 - линейное непрерывное звено без учета квантованное™ в соответствии с выражением (8.2). Все сказанное в отношении АЦП распространяется и на ЦАП лишь с тем отличием, что входной величиной ЦАП является безразмерная цифровая переменная у, а выходной - размерная квантованная по уровню переменная х. Следовательно, *сР = кЦАПу,(8.9) где кти = Ах0 - передаточный коэффициент ЦАП (Дх0 - дискретная единица выходной переменной ЦАП). Выбор той или иной расчетной модели АЦП или ЦАП можно выполнить по уровню искажения полезного сигнала, проходящего через квантованный преобразователь. Уровень искажения оценивается отношением «полезный сигнал - шум» ks=T(8Л0> где хт - амплитуда синусоидального полезного сигнала; Дхпт - амплитуда эквивалентной синусоидальной помехи квантования - Ах0, (A-*rim - y2xn - ), и в логарифмическом масштабе 4=201g*,.(8.11) Величины к5 и Ls связаны с числом уровней дискретности N и числом разрядов п преобразователей: N = L = 0n i 2-1 + а 2«-2 +... + а, 2°,(8.12) Дх0 где хтах - максимальный выходной сигнал преобразователя. Для n = const Nmm = 2-1 = I 2", NmiX = 2" - 1 = 2iVmin - 1. Для полезного сигнала, равного максимальному выходному сигналу преобразователя, ks = J6N. Чем больше к„ тем меньше искажения, вносимые в полезный сигнал квантованных преобразователей, тем большее число уровней дискретности у него требуется. Можно выделить два значения ks - ksm3X и ksmin, такие, что если ks > ksmax, то ошибка от квантования пренебрежима мала и используется модель 3; если ks < ksmin, то ошибка от квантования соизмерима с полезным сигналом и используется модель 1; если ksmin < ks < ksmax, то ошибка от квантования заметна, но может учитываться приближенно с использованием модели 2. Оценить количественно граничные значения к1тахи ksminможно лишь с определенной долей условности. Так, принимая точность измерения полезного сигнала Ахт = 1 %, получим A-smax = 100. При к, > 100 амплитуда помехи от квантования Дхпт будет меньше ошибки измерения сигнала хт и квантованностью по уровню можно обоснованно пренебречь. Если принять значение ksmin = 10, то при ks< 10 помеха от квантования Дх1Ш составит более 10 % от сигнала хт, т.е. будет соизмеримой с полезным сигналом, и потребуется уточненная расчетная модель 1. Если для регулируемой координаты электропривода задана допустимая ошибка Дхдоп, то влияние квантования по уровню можно оценить по значению ошибки Дх регулируемой координаты от воздействия помехи Ах„: Ах = А:Ах0 < 0,1Дхдоп - квантование не учитывается (модель 3); Ах = кАх0 > АХд011 - квантование полностью учитывается (модель 1); 0,1Дхдо„ < Дх = кАх0 < ДхД0, - квантование учитывается интегрально (модель 2). J! . цг~ II Ип (7е0)] da. 12rtJ0 8.3. Дискретные передаточные функции и структурные схемы контура регулирования электропривода Цифровые СУЭП с программным способом управления строятся на основе универсального управляющего устройства - микроЭВМ (рис. 8.3). Все необходимые функции ЦСУ - формирование задающего сигнала х3, сравнение с сигналом обратной связи Ах = х3 - х, формирования алгоритма управления у - после предварительной загрузки некоторых начальных параметров хз0 выполняются расчетно, последовательно по программному циклу микроЭВМ, занимающему интервал времени Тр. В данный цикловой период входят временные интервалы считывания показаний датчиков, расчета алгоритма, реализации сигнала управления. Исполнительная часть СУЭП - управляемый преобразователь УП может быть как непрерывным, так и дискретным с некоторым временным интервалом дискретности Ти (например, управляемый 0 ... 39 40 41 42 43 44 45 ... 49 |












