Раздел: Документация
0 ... 42 43 44 45 46 47 48 49 <ЦРТ L т 1 т Т„ R„ 1-1 ТЛк к Т к к 1 лп1о.т *т по.т VPT интегральная часть £црт(1-я) 1 1- L 71 .лцрт , гг , Таким образом, только при условии Г «с Тх и Г«: Гя параметры ЦРТ оказываются практически равными соответствующим параметрам аналогового РТ. При настройке цифрового контура тока на модульный оптимум (Тт = 2ТП = 2Т) отмеченное выше условие малости параметра Ти относительно Тт нарушается и значения параметров ЦРТ отличаются от параметров аналогового РТ. По полученной ДПФ ЦРТ z-dx . (l-d„)z~l Y(z) Ттр WrFT(z) = knPJ- 7-1 = к црт 1 X(z) может быть составлена структурная схема данного регулятора (рис. 8.10). При подаче на вход ЦРТ скачкообразного входного сигнала х[п] = х01[и] выходной сигнал будет определяться разностным уравнением у[п] = кЦРТх[п] - кпях[п -1] + у[п -1].(8.56) Выходной сигнал у[п] линейно возрастает от начального значения у0 =кЦРГх0 с приращением на каждом последующем такте Ау = £ЦРТ(1 - djxo (рис. 8.11). Цифровой сигнал регулятора тока у[п] поступает на вход цифрового СИФУ, вырабатывающего цифровые сигналы угла открывания Na и номера очередного тиристора NT, на который должен быть подан управляющий импульс. Достоинства цифрового контура тока: возможность получения высокого быстродействия с временем переходного процесса в пределе в один интервал дискретности ТП при достаточно высо- [и]
уЫ Цифровое СИФУ N„ 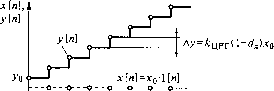 1 2 3 4 5 6 7" Рис. 8.11. Отработка скачка входного сигнала цифровым ПИ-регулятором ком быстродействии цифровой вычислительной машины; возможность прямого цифрового управления, при котором все функции управления регуляторов и СИФУ могут быть реализованы программно на единой унифицированной элементной базе - микропроцессорной системе. 8.6. Оптимизация цифрового контура скорости Данную оптимизацию будем рассматривать применительно к структуре подчиненного регулирования координат, когда в составе контура скорости имеется предварительно оптимизированный цифровой контур тока. Задача оптимизации сохраняется той же, что и для контура тока, - синтез цифрового регулятора скорости (ЦРС), обеспечивающего желаемые динамические показатели контура, которые соответствуют выбранному уровню оптимальности. Синтез ЦРС выполняется для динамики «в малом», когда электропривод принимается за линейную импульсную систему. Структурная схема цифрового контура скорости представлена на рис. 8.12. В ее состав входят: ДПФ ЦРС Wnvc (7), подлежащая определению; ДПФ замкнутого цифрового контура тока »;т(0 = -- = - Act3T(7) k0T z-dT передаточные функции экстраполятора, интегрирующего звена, датчика обратной связи по скорости, АЦП. За входную переменную принято приращение задающего угла Дазс для тиристорного преобразователя. Выходной физической переменной контура является приращение скорости Дсо, а за расчетную выходную переменную для выполнения синтеза принят сигнал датчика скорости, выраженный в приращении угла ТП Да0 с. В соответствии со структурной схемой ДПФ приведенной непрерывной части контура Wn (7) =1Z {hm [„]}.(8.57) Да, 1 Да, с [и] Ицрс(г) 1 l-rf,. А/И 1 г-1 Дсо Дас с [и] 1 Да„ сацп Д"о Рис. 8.12. Структурная схема цифрового контура скорости Из таблицы для изображений решетчатых функций для hm[n] = пТ находим Тогда Здесь Z{hH3[nT]} Wn{z) Tz (z-l)2 (z-dT)(z-D (8.58) (8.59) k0T TMkPC 2TT где ka - передаточный коэффициент двигателя, радДВс); Ти - механическая постоянная времени электропривода, с; к о.е = о.сАЦП- Выражению (8.58) соответствуют согласно (8.33) v„ = 1; Q(z) = = Z-dT; P(z) = P0. Оптимизацию контура скорости выполним методом стандартных уравнений с желаемым распределением корней характеристического полинома. Принимая для первого варианта синтеза статическое регулирование скорости, т.е. желаемый порядок аста-тизма v = 1, будем иметь в области непрерывных переменных желаемый характеристический полином второго порядка АкелЫ = Р2+ С\ЩР + COg ~ (Р ~ Pl)(P ~ Pi)- V2 Для модульного оптимума с, = V2; А,2 = -а ± yQ = -- соб(1 ± j); 1 1 T"" = 28;c°6 = V27;"2V27;- Определим соответствующий модульному оптимуму характеристический полином для дискретных переменных в области z = е Акел(г) = (ерТ - е?>т)(е»т - ет) = = е2рТ - ерТ 2е~аГ cos D.T + е~2аТ =(8.60) = z2 +dxz + d2, где dx = -2еаТ cosQT = -1,509; d2 = е~2аТ = 0,606. При этом cos = -pi- = -£=-; аТ = i; QT = -. 42Tm 242T44 Выполним синтез на основе уравнения реализуемости (8.36): P0M(z) + (z- l)N(z) = z2+dlZ + d2. Определим порядки искомых полиномов M(z) и N(z): lM+ lP< I = 2, следовательно, lM< 1; M(z) = m0; lN+ v = / = 2, следовательно, lN= l-v = 1; N(z) = n0z + щ. Отсюда P0m0 + (z- l)(n0z + щ) = z2 + diz + d2. Методом приравнивания коэффициентов при равных степенях z находим коэффициенты полиномов M(z) и N(z). Из равенства коэффициентов при z2 следует, что щ = 1; из равенства при zu-я, - «о = du п{ = di + 1; из равенства при z°: р0т0 - и, = с/2, та = = (d2 + di + 1)/п0. Тогда = /ио = (1 + rf+</z); ад = z + 1 + dv "о Согласно (8.38) ДПФ ЦРС и/ )Q(z) l + c/,+cf2 z-dT WnPciz) ~ (z-iy-N(z) ~ P0 z + l + di (8-61) Для принятой настройки на модульный оптимум с учетом значений du d2, dT 0,097 г-0,606 ЦРс(") />0 г-0,509"(8-62) Полученной ДПФ ЦРС соответствует ДПФ замкнутого цифрового контура скорости (ЦКС) W(Z) = Р(г)М(г) ==1 + 4 + d2/g 63ч Акел(г) z2+diz + d2 z2 -1,509*+ 0,606 Из выражения для ДПФ ЦРС (8.62) следует, что для получения в ЦКС модульного оптимума требуется цифровой регулятор, отличный от пропорционального. Из уравнения (8.61) очевидно, что для получения пропорционального ЦРС достаточно выполнить условия zL dx = -(l + dT) = -(l-eT* ) =-1,606; d2 = 0,097+ = 0,703. Тогда pc(.) = 4- = .(8-64) "о"о Изменение коэффициентов dx и характеристического полинома DMtJI(z) приводит к изменению его корней аТ= 0,176, QT = = 0,293 и, следовательно, к нарушению условия модульного оптимума. Однако можно ожидать, что это вызовет относительно небольшое ухудшение динамических показателей, так как корни изменились относительно немного и при синтезе по уравнению реализуемости учитывалось условие «грубости» системы. Время переходного процесса цифрового контура определяется выбранным значением базовой частоты СО1 = Тп.п и составляет для данного цифрового контура скорости *пл = 2>/2Гтп.п =7,91Г, т.е. приблизительно восемь тактов дискретности тиристорного преобразователя. Сравним передаточные коэффициенты цифрового (&ЦрС) и аналогового (кРС) регуляторов скорости: кцрс = l±A±A = *рс f1- « 0,99*РС. (8.65) Таким образом, передаточные коэффициенты цифрового и аналогового регуляторов скорости практически совпадают при настройке на модульный оптимум. Однако при этом ЦРС несколько отличается от пропорционального регулятора, как видно из ДПФ (8.62). Аналогично выполняется синтез ЦРС для варианта астатического регулирования скорости, когда желаемый порядок астатизма контура скорости v = 2. В этом случае характеристический полином замкнутого контура скорости имеет третий порядок. Выбирая желаемый характеристический полином с настройкой на модульный оптимум и оптимизируя контур скорости методом уравнения реализуемости аналогично рассматриваемому выше, получаем ДПФ ЦРС: w = M(z)Q(z) = (mpZ + mjz - dT) = црс (z-iy-*»N(z) (z-l)(z + d1+2)(8 66) 1 (0,12z -0,106)(z- 0,606) Р0 (*-l)(z-0,50) Полученная ДПФ ЦРС соответствует ДПФ замкнутого цифрового контура скорости согласно (8.34) (d2 + 2dx + 3)7 + d3 - dx - 2 w(z) z3 +dxz2 +d2z + d2 0,127-0,106 (8.67) 73 - 2,5072 + 2,127 - 0,606 В установившемся режиме, когда 7=1, w(z) = 1. Полученная структура ЦРС обеспечивает астатическое регулирование скорости в сочетании с оптимальным демпфированием. Время переходного процесса составляет ?п.п= - = 47\,П=23,6Г*24Г, С0б т.е. оказывается существенно больше, чем при оптимизации со статическим регулированием скорости. Реализация ЦРС с ДПФ, соответствующей выражению (8.66), вызывает определенные трудности. Структура ЦРС существенно упростится и будет соответствовать цифровому ПИ-регулятору, если выполнить условие dx = -(dT+2). Однако при этом нарушится принятое условие оптимальности. Насколько это допустимо, можно определить сравнением переходного процесса для замкнутого контура скорости с измененными коэффициентами характеристического полинома с оптимальным переходным процессом. Цифровое управление током и скоростью электропривода позволяет оптимизировать его на минимум времени переходного процесса, который завершается за конечное время, т. е. за конечное число тактов. Так, для статического регулирования скорости с характеристическим полиномом второго порядка можно минимизировать время переходного процесса согласно уравнению (8.40) до двух тактов дискретности ТП, если выбрать в качестве желаемого полинома А*ел(<0 = Z2- Тогда уравнение реализуемости будет иметь вид />0М(7) + (7-1)лг(7) = 72. Выполняя процедуру определения полиномов M(z) и N(z), получаем M(z) = m0= l/P0; N(z) = n0z + nl = z+ 1. ДПФ ЦРС »WO = M(Z)Q(Z) =(8.68) Ц(Z-\)v-v"N(z) Р0 7+1 0 ... 42 43 44 45 46 47 48 49 |












