Раздел: Документация
0 ... 8 9 10 11 12 13 14 ... 49 после преобразования в аналоговые сигналы выделяются усилителем как напряжение управления Uy, имеющее одно из трех значений: -Uy, Uy, 0. Достоинствами логической формы алгоритма управления можно считать простоту ее выражения и отсутствие требования иметь аналитическое описание объекта управления. Недостатками приведенного алгоритма являются колебательный характер движения положения равновесия и возникновение режима автоколебаний при моменте трения, равном нулю. Причина колебаний вокруг положения равновесия - отсутствие необходимого управления в зоне, где Uy = 0. Это следствие ограниченной регулирующей возможности двухуровневой жесткой логики. Недостаток данного алгоритма, построенного на основе классической жесткой логики, можно устранить, если использовать так называемую фаззи-логику. На ее основе можно обеспечить устойчивое высококачественное позиционирование и при отсутствии момента трения. Данная глава посвящена понятию и принципам фаззи-логики и системам фаззи-управления электротехническими объектами на ее основе. Фаззи-логика в переводе с английского - нечеткая, нежесткая, приближенная логика. Родившаяся в 60-е годы прошлого века как развитие теории множеств применительно к информационным системам [30], она находит сегодня все большее применение в различных технических системах как средство управления. Применительно к электроприводу фаззи-логика используется для определенного класса задач управления как нижнего, так и верхнего уровней. Что же такое фаззи-логика (ФЛ) и чем она отличается от классической логики, начала которой были заложены еще древнегреческим философом и ученым Аристотелем? Классическая логика с двумя качественными или количественными уровнями (истинно-ложно, да -нет, единица -ноль) не позволяет описать многообразие, многоцветность мира и ассоциативный (объединяющий в общие понятия) способ мышления человека. Этот пробел выполняет ФЛ, использующая многоуровневое представление физических величин и утверждений (табл. 4.1). В классической логике физические величины и утверждения делятся жестко, бескомпромиссно на два уровня. В фаззи-логике кроме крайних двух уровней имеются и промежуточные, при этом переход от одного уровня к другому не резкий, а с перекрытием соседних уровней. Для определенных физических величин и фактов их двухуровневое классическое представление «истинно-ложно», «да -нет» полностью справедливо и точно. Например, на вопрос, движется ли рабочий орган, можно ответить только однозначно «да» или «нет». Но на вопрос, как движется рабочий орган (быстро, медленно, очень медленно), двухуровневая логика не дает ответ, а фаззи-логика позволяет его получить. Таблица 4.1 Примеры уровней в классической и фаззи-логике
Выделение уровней в логике - это ассоциативное свойство мышления человека, когда качественная характеристика физических величин и процессов, формируемая словесно (прилагательными, наречиями), оценивается количественно не отдельными числами, а некоторыми числовыми множествами с нерезкими границами. Фундаментальным понятием фаззи-логики, введенным ее основоположником американским профессором электротехники Л. Заде, является фаззи-множество (ФМ). В математической логике есть общее понятие множества как совокупности объектов, каждый из которых должен обладать или не обладать определенным свойством. Это множество характеризуется только одним показателем, все его объекты равноценны относительно определяющего его свойства. В отличие от данного понятия множества фаззи-множество характеризуется двумя показателями, во-первых, фактом принадлежности объектов к множеству и, во-вторых, степенью их принадлежности к данному множеству. Применительно к техническим системам объектами ФМ являются значения некоторой физической переменной, например, значения температуры, скорости перемещения, электрического напряжения, тока и т.д. Словесное (лингвистическое) выражение физической переменной считается логической переменной в фаззи-логике. Свойством, объединяющим значения физической переменной в ФМ, является выделенная некоторая качественная оценка в лингвистической форме для логической переменной, например, отрицательная малая (NS), нулевая (Z), положительная средняя (РМ), положительная большая (РВ) и т.п. Данные качественные оценки ФМ uOc)
Рис. 4.2. Пример фаззи-множеств и функций принадлежности называются термами. Степень принадлежности значений физической переменной х к ФМ, к данному терму, определяется так называемой функцией принадлежности (ФП) д(х). Значения ФП определяются в пределах от 0 до 1 на интервале от х = а, где д(а) = 0, до х = Ъ, где \х(Ь) = 0. Внутри интервала [а, Ь] есть точка х = с, где д(с) = 1. По своему виду функция д(х) напоминает функцию распределения вероятности принадлежности значений х интервалу [а, Ь] с максимумом плотности вероятности, равным 1 в точке х = с и с плавным уменьшением от 1 в обе стороны до 0. Сходство д(х) с функцией распределения вероятности лишь внешнее, а по существу, определение параметров ФП (формы, места расположения центра с и границ интервала х) возлагается на эксперта в соответствующей области. Физическая переменная на заданном интервале X ее изменения от xmin до хтах характеризуется рядом ФМ (Ах, А2, А„) с функциями принадлежности дх), д„(х). На рис. 4.2 в качестве примера переменная температура помещения представлена термами: положительная низкая (PS) для х= Г=4...17°С; положительная средняя (РМ) для х = 12...27"С; положительная высокая (РВ) для х > 23 "С. Выделенным ФМ Ах, Аъ Аъ соответствуют ФП дДх), д2(х), д3(х) с центрами с,, с2, с3, в которых д(х) = 1. Сама суть фаззи-логики в ее нежесткости и приближенности обусловливает наличие участков перекрытия термов [а/+1, Ь], где нарушается однозначность принадлежности значений переменной х только одному терму. Ширина участков перекрытия может быть различной, в пределе и нулевой. Но максимальная ширина ограничивается очевидным условием: там, где для одного терма д,(х) = 1> Для другого может быть 1 > д,±1(х) > 0 с исходным условием u,+i(x) = 0. При построении ФП приоритетное значение приобретает расстановка центров ФП, где имеет место д(с,) = 1, что означает бесспорную принадлежность значения х = с, к соответствующему терму. Если ФП для температуры помещения составлены экспертом-медиком, то температура Г= 20 °С как наиболее комфортная для самочувствия человека будет принята за среднюю, Т= 10 °С - за бесспорно низкую, когда требуется включение обогревателя, а 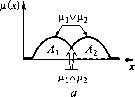 Ml Н2 Ш *2 б Рис. 4.3. Операции усреднения и объединения фаззи-логики для одной переменной (а) и для двух разных переменных (б) Т = 30 °С - за бесспорно высокую, когда требуется включение кондиционера. При Т= С, температура относится одновременно к двум термам PS и РМ, поэтому возникает проблема, какое из двух значений ФП принять. Данная проблема решается компромиссно на основе принципов совмещения множеств, известных из математической логики, в форме трех операций: усреднения, или конъюнкции, К(цх, ц2) = д, л д2 = min(u,(x), Ц2W)- принцип минимума; объединения, иди дизъюнкции, D(\xu д2) = д1 v д2 = max(\xx(x), Ц2М)- принцип максимума; инверсии или дополнения, д(х) = 1 - д(х). Операции К(\хи д2) и D(ix{, д2) взаимосвязаны: ДЦь Д2) = 1 - D(\xu д2); 2)(дь д2) = 1 - К([хъ д2). Результат операций усреднения и объединения фаззи-множеств Ау и А2 одной переменной х приведен на рис. 4.3, а. Штриховая линия означает конъюнкцию двух ФП (д, л д2), сплошная линия - дизъюнкцию двух ФП (ц, v д2). Операции усреднения и объединения ФМ Ац и A2J двух разных переменных х, и х2 выполняются в каждый фиксированный момент времени th когда х, = ,(г,) и х2 = i(t,), также по принципам минимума (д1(,) л д2(2)) и максимума (i() v ц2(2)) (рис. 4.3, б). Аналогичные операции могут применяться и для большего числа ФМ и переменных. Приведенные выше операции позволяют принять одно определенное значение функции принадлежности в зоне взаимного перекрытия фаззи-множеств. Это дает основание для принятия определенного решения и относительно значения выходной переменной у, являющейся управляющим воздействием в системе с фаззи-управлением. 4.2. Структура и алгоритм фаззи-управления Фаззи-логика является основой некоторых интеллектуальных систем управления. К интеллектуальным относят сегодня многие системы управления, в том числе те, которые в той или иной форме имитируют систему мышления человека с целью решения технических, экономических, информационных задач. Так называемые нейронные сети на компьютерном уровне моделируют приближенно структуру мозга человека. Ценное свойство нейронных сетей, вытекающее из мозговой деятельности человека, - обучаемость, следовательно, с помощью определенного правила можно обучить систему преобразовывать входные воздействия (данные) в желаемые выходные действия (данные). На основе этого свойства нейронные сети рассматривают как универсальный ап-проксиматор, способный реализовывать любые преобразования входных воздействий или данных в выходные. К другому типу интеллектуальных систем управления относятся системы с фаззи-управлением. В этих системах моделируется не структура мозга человека, как в нейронных сетях, а процесс мышления человека - процедура принятия им решения. Схема данного процесса такова: оценка условий ситуации - их восприятие - принятие решения (логическое заключение) на основе базы знаний - исполнение. Например, ЕСЛИ реактивный ток цеховой подстанции положительный большой, ТО ток перевозбуждения синхронного компенсатора дать большой; ЕСЛИ температура воздуха положительная низкая И влажность высокая, ТО ток электронагревателя дать средний; ЕСЛИ давление в котле выше нормального ИЛИ температура очень высокая, ТО топливный вентиль закрыть. В более кратной форме можно записать: ЕСЛИ х есть А, ТО у есть В; ЕСЛИ х{ есть Ах И х2 есть А2, ТО у есть Вх; ЕСЛИ х, есть Ах ИЛИ х2 есть А2, ТО у есть В2. Здесь выражения «х есть А», «у есть В» означают, что значение переменной х принадлежит фаззи-множеству (ФМ) А, значение переменной у принадлежит ФМ В. Приведенные записи в развернутой или в свернутой формах представляют собой правила, определяющие взаимосвязь входных и выходных переменных функций фаззи-логики. Как и в классической логике, в фаззи-логике логические функции формируются операторами конъюнкции (И) или дизъюнкции (ИЛИ), но не с числами 0 и 1, а с ФМ А-, и В}. Приведенная третья форма правила с двумя входными переменными х, и х2, объединенными оператором ИЛИ, может быть заменена первой формой правила для каждой переменной в отдельности: ЕСЛИ х, есть Ах, ТО у есть В; ЕСЛИ х2 есть А2, ТО у есть В. Поэтому основной формой правил для многих входных переменных остается их усреднение, т.е. конъюнкция: ЕСЛИ 5, е АХА И l%2 е А2Л И ... И \%„ е АпМ, ТО г, е Bj, (4.1) где %и cj2, „ - измеренные конкретные значения фазических входных переменных хх, х2, х„; AXJX, A2J2, АпАп - термы входных переменных (первый индекс означает номер переменной, а второй - номер терма); л - вычисленное конкретное значение физической выходной переменной у; Bj - терм с номером j выходной переменной. Набор соответствующих выражению (4.1) правил является алгоритмом фаззи-управления. Какова общая структура фаззи-управления? Как и в любой традиционной системе, в ее составе можно выделить управляющую часть - систему управления, и объект управления. Собственно система фаззи-управления состоит из четырех блоков, выполняющих последовательно в три этапа процедуру формирования алгоритма управления как функции управляющих воздействий у от входных переменных х,, х2, х„ (рис. 4.4). Блок фаззификации (Ff) преобразует входные физические переменные (хх, х2, х„) в термы А,- лингвистических переменных и выделяет для каждого момента времени (для каждого временного такта) значения ФП ц,(х) для активизированных правил. Блок логического заключения (Inf) в соответствии с правилами, заложенными предварительно экспертом в блок базы знаний (RAM), определяет термы тЗ, выходной лингвистической переменной и присваивает им согласно принципам ФЛ значения функции принадлежности Цу(у). Блок RAM
0 ... 8 9 10 11 12 13 14 ... 49 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












