Раздел: Документация
0 ... 12 13 14 15 16 17 18 ... 49 У}~ Cj\X\ + cj2x2 + ••• + Cj„Xn, гдеу = 1, г. Уравнение модального регулятора: Upj = kj\X\ + kj2x2 + ... + kjnxn, гдеy=l, т. Уравнение замыкания: Uj=Vj-UvJ, гдеу = 1, т. Описание системы с модальным управлением п + г+т уравнениями более компактно представляется в матричной форме: X(t) = AX(t) + BU(t); Y(t) = CX(t);(5 1} Uv(t) = KX(t); U(t) = V(t) - Up(t), где A - квадратная матрица объекта управления (пхп), А = [а1;]; В - прямоугольная матрица управления (пхт), В= [Ь0]; С - прямоугольная матрица выходов (гхп), С= [с]; К - прямоугольная матрица модального регулятора (т хп), К= [к0]. Для замкнутого по вектору состояния ОУ первое, третье и четвертое уравнения системы (5.1) совместно дают результирующее матричное уравнение во временной области: X(t) = (А- BK)X(t) + BV(t).(5.2) Уравнениям (5.1) и (5.2) соответствует векторно-матричная схема (рис. 5.2). Уравнение (5.2) в операторной форме имеет вид DX(p) = BV(p),(5.3) где D - характеристическая квадратная матрица (пхп); D = pl-A + BK,(5.4) где I - единичная матрица. V(t) U(t) о в Off X(t) О IIP к с Рис. 5.2. Векторно-матричная схема системы модального управления 94 Детерминант от матрицы D является характеристическим полиномом замкнутого по ВС объекта управления: D(p) = detCpI - А + ВК) = £ (-1)+ЧА,(5.5) где / - номер строки; у - номер столбца; di} - элемент /-й строки и у-го столбца характеристической матрицы; Dy - минор, соответствующий элементу di}. Решение характеристического уравнения D(p) = 0 дает корни ОУ, замкнутого по ВС. Так как корни определяют динамические свойства системы, замкнутой через MP, то для получения желаемых динамических показателей потребуются соответствующие корни характеристического полинома. Отсюда вытекает принцип синтеза модального регулятора: подобрать матрицу К модального регулятора так, чтобы получить в комплексной плоскости желаемое распределение корней характеристического полинома замкнутого по вектору состояния объекта управления. Синтез MP выполняется методом стандартных уравнений, которые в нормированной форме приведены в справочной литературе. Для получения нормированной формы исходное уравнение л-го порядка D(p) = Dqp" + DlP"-1 + ... + D-+Dp + D„ = 0 делится на коэффициент D0 и приобретает корневую форму р" + сущр"~{ + ... + С/СОР""1 + ... + c„ !tOe = 0.(5.6) Здесь соб - базовая частота (среднегеометрический корень), Делением уравнения (5.6) на сое осуществляется переход к нормированному уравнению Sn + cxSn~{ + ... + c,S"i+ ... + ся ,5+1 = 0(5.7) с относительным оператором S = - = -у- и относительным вре- соб ат менем т = oV. В табл. 5.1 приведен некоторый набор нормированных уравнений со второго по шестой порядок [18]. Каждое приведенное уравнение характеризуется определенным распределением корней, которому соответствуют значения перерегулирования а и относительного времени переходного процесса т„ п при отработке замкнутым по ВС объектом управления скачка задающего сигнала. Таблица 5.1
5.1.2. Синтез модального регулятора электропривода Полученная на основании математического описания вектор-но-матричная схема системы с модальным управлением представляет собой при отсутствии внешних воздействий замкнутый 96 контур, состоящий из двух частей - объекта управления и управляющего устройства, называемого в данной системе модальным регулятором. Каждая из этих двух частей характеризуется соответствующими матрицами. Модальный регулятор преобразует вектор состояния X(t) объекта управления в вектор управления U(t). Цель синтеза MP согласно сформулированному в подразд. 5.1.1 принципу заключается в соответствующем подборе матрицы К, т.е. в определении параметров MP, обеспечивающих желаемые показатели качества объекта управления, замкнутого по ВС. К показателям качества относятся: перерегулирование а, характеризующее уровень демпфирования системы или уровень плавности движения рабочего органа; время переходного процесса tnn, характеризующее быстродействие системы; жесткость рз или статизм 83 механической характеристики, когда объектом управления является электропривод. Процедура выполнения синтеза MP методом стандартных уравнений осуществляется в три этапа. 1.Определение количества и выбор переменных состояния, составление относительно выходной координаты характеристических уравнений для разомкнутого объекта управления (ОУ) т (d0p" +dlp"-1+... + dip"-< +... + dn lp + d„)xH=Zbi(p)Ul (5.8) и ОУ, замкнутого по ВС, т (D0p"+DlP"-> +... + Dlp"-1 + ... + DnAp + Dn)x„ =XBf(P)V,. (5.9) i=i В уравнениях (5.8) и (5.9) х„ - выходная переменная состояния; т - число воздействий на ОУ; Do = d0; A=4 + f>A,(5.10) где Oj - параметр ОУ поу-й переменной состояния; kj - коэффициент усиления MP по у-й переменной состояния. 2.Выбор по желаемым показателям качества (о и тпп) нормированного уравнения (5.7), порядок п которого равен порядку уравнения объекта управления. 3.Определение параметров MP из системы уравнений п A =di+?Z ajkj = Ажел = 4>C/00fe,(5.11) У=1 где / = 1, п. 4 Терехов 97 В системе из п алгебраических уравнений (5.11) известными являются параметры aj} d0, dh с,, а искомыми - к}. Если задано желаемое быстродействие системы /1М1.жел, то базовая частота оказывается известной и равной юб = т„ u/tn п жел. В этом случае система уравнений (5.11) оказывается линейной, решение ее дает искомые значения параметров MP kj. При этом установившийся режим объекта управления характеризуется уравнением (5.9) при подстановке в него р = 0: D„x„ =ХД,(0)К,.(5.12) ы Для электропривода из уравнения (5.12) может быть определена жесткость его механической характеристики (рз), которая оказывается функцией kj, т.е. рз = f(kj), и значение которой может быть недопустимо низким - Р3 < РЖеЛ- Чтобы обеспечить желаемое значение жесткости, систему уравнений (5.11) следует дополнить уравнением р3 = /(kj). Тогда в числе искомых величин будет дополнительно юб. Однако при этом система уравнений (5.11) становится нелинейной и ее решение при высоком порядке п представляется непростой расчетной задачей. Практически данную задачу проще решить, задавая ряд значений соб и определяя соответствующие им значения рз. Таким образом, в синтезе модального регулятора динамические и статические показатели взаимосвязаны. Обеспечивая желаемые динамические показатели ажел, ?п.п.жел, получаем подчиненный им статический показатель рз, и наоборот, задавая желаемые значения ажел и рхел, получаем подчиненное им значение ?„,,. Выполним синтез MP для электропривода с упругим механическим звеном. Таким звеном может быть кинематическая цепь (КЦ), передающая механическую энергию от вала двигателя (Д) к рабочему органу (РО) и обладающая заметной упругой податливостью (длинный вал, редукторная передача, канатная, цепная, ременная передачи). Упругое звено с коэффициентом жесткости С,2 связывает между собой две массы (ротора двигателя и рабочего органа), характеризуемые при вращательном движении моментами инерции /, и /2. Структурно электропривод с таким звеном представляет собой двухмассовую электромеханическую систему (ДЭМС) (рис. 5.3), которой при определенном соотношении параметров присущ резко колебательный характер движения. Задача управления для данного электропривода состоит в обеспечении устойчивости, стабилизации движения рабочего органа в динамических и статических режимах. Синтез MP для приведенной на рис. 5.3 структуры выполним на базе электропривода постоянного тока с инерционным управляемым преобразователем (УП) с коэффициентом усиления ки и постоянной времени Ти и безынерционным усилителем (У) с ко- №„ Та) (Гз./о (с12) 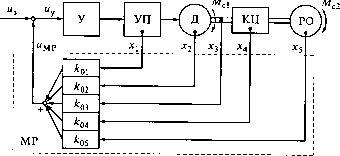 Рис. 5.3. Структура двухмассовой электромеханической системы с модальным регулятором эффициентом усиления кт Моменты сопротивления МсЬ Мс2, скорость рабочего органа РО со2 и параметры подвижной части /,, /2, С,2 приведены к скорости двигателя со,. Электропривод описывается исходной системой уравнений (Тпр + 1)еп = кпкуиу; (7> + Г)/ = 1(еп --p<»i); JiP®i =T-i-Mc-Mn; k»(5.13) Mn = Ci2(<Pi -Фг); J2pco2 = Mn-Mc2; со, = рщ; со2 = РЦ)2, где еи - ЭДС УП, В; Тэ - электромагнитная постоянная времени, с; / - ток якоря двигателя, A; R - сопротивление якорной цепи, Ом; Ка - передаточный коэффициент двигателя, радДВс). Согласно процедуре синтеза выбираем переменные состояния: xi = ем х2 = ! х3 = со,; х4 = Ml2; х5 = со2 и, решая систему уравнений (5.13) относительно выходной координаты со2, получаем уравнение разомкнутого электропривода: (d0p5 +dxp4 +d2pi +dip1 +d4p + d5)tu2 = = -4,4V+V3+V+V+65),(5H) где kn - передаточный коэффициент разомкнутого электропривода (kQ = kyknka). 0 ... 12 13 14 15 16 17 18 ... 49 |












