Раздел: Документация
0 ... 31 32 33 34 35 36 37 ... 49 управления по сравнению с системами, где используется косвенный (расчетный) путь определения сигналов обратных связей. Если при определении момента воспользоваться выражением М = \рп[2хЦ,(6.42) где L2 - индуктивность обмотки ротора, приведенная к цепи статора, то в качестве регулируемых будут выбраны векторы Ч?2 и 1\-Их векторные диаграммы при ориентации Ч?2 по оси х системы координат х, у представлены нагрис. 6.35, Здесь же показаны векторы токов намагничивания /м, ротора Г2 и проекции векторов тока статора и ротора на оси х, у и а, В. При этом 2х = Ц.2х + hlhx - 2 >2у = ЦЦу + Ц21\у = О Г2х = 0;Г2у = -«Онома/Ь т.е. в установившемся режиме вектор тока ротора 72 перпендикулярен вектору Ч/2, отстает от него на угол 90 эл. град., а его модуль при ЧУ2 = const меняется пропорционально абсолютному скольжению. В двигательном режиме вектор тока статора 7Х опережает вектор Ч/2 на угол 0 = arctg(L2(£>UKOlisJR2), его составляющая IXx = = y¥2/Ll2 определяет потокосцепление ротора Ч/2, а составляющая Ily = x¥2L2o}0homsJ(L12R2) компенсирует влияние на него реакции ротора. В соответствии с выражениями (6.42) и (6.43) электромагнитный момент АД определяется взаимодействием ортогональных составляющих потокосцепления ротора Ч?2 = ЧУ2дг = LnIlx и тока статора Таким образом, при стабилизации Т2, как и при стабилизации ЧУЦ, система векторного управления будет подобна системам управления двигателями постоянного тока, где составляющая 1Хх тока статора определяет потокосцепление Ч?2 АД (магнитный поток ДПТ), а составляющая 1[у является моментной составляющей тока статора (аналогично току якоря ДПТ). Векторные диаграммы на рис. 6.35 позволяют дать физическую интерпретацию принципа построения систем векторного управления АД по аналогии с управлением машиной постоянного тока. Так, в системах управления с ориентацией вектора потокосцепления ЧУ2 по оси х при отсутствии задания скорости АД и статической нагрузки на его валу (Мс = 0) должно обеспечиваться задание исходного потокосцепления Ч*2 лишь за счет составляющей тока статора 1Хх. При этом вектор тока статора равный по модулю току 11х, будет совпадать по направлению с вектором Ф2, равным по модулю потокосцеплению *F2v. Если подобного совпадения не произойдет, то появление составляющей 1Ь, ф 0 приведет согласно выражению (6.42) к возникновению электромагнитного момента Мф 0 и при Мс = 0 начнется движение вала ротора АД. Тогда за счет обратной связи по скорости (либо по ЭДС) двигателя система должна обеспечить фазовый поворот вектора /, до его совпадения с вектором Ф2, при котором электромагнитный момент станет равным нулю и произойдет останов двигателя. При неподвижном роторе (/, = 0, асо0ном = 0) и отсутствии статической нагрузки вектор ¥2 будет неподвижным в пространстве, а ток 1Х - постоянным во времени. Система координат х, у также будет неподвижна. Подобное состояние АД аналогично условию подачи постоянного тока в обмотку возбуждения ДПТ без подключения его якорной цепи к источнику напряжения. При поступлении сигнала задания скорости АД система управления сначала обеспечивает поворот вектора 1Х относительно Ф2 и, в итоге, возникновение электромагнитного момента МфО, под действием которого при М> Мс начинается движение вала ротора АД. Это движение будет происходить до тех пор, пока реальная скорость АД не сравняется с заданным значением. При их равенстве вектор 1Х вновь устанавливается по направлению вектора у¥2, а электромагнитный момент становится равным нулю. Однако в отличие от предыдущего режима ток статора является уже переменным во времени, а вектор Ч?2 вращается в пространстве со скоростью, пропорциональной частоте тока. С той же скоростью вращается и система координат х, у. Поэтому составляющие 11х и Ч,2х остаются на прежнем уровне. АД работает в режиме идеального холостого хода со скоростью, также связанной с заданной частотой тока статора. Подобное состояние АД аналогично режиму идеального холостого хода ДПТ, когда при постоянном его возбуждении и Мс = 0 якорная цепь ДПТ подключена к регулируемому источнику постоянного напряжения. При увеличении нагрузки на валу АД система управлениядол-жна обеспечивать поворот вектора 1Х относительно вектора Ф2 таким образом, чтобы, во-первых, составляющая /оставалась неизменной, сохраняя постоянство потокосцепления Ч7, а, во-вторых, составляющая 11у увеличивалась до значения, при котором электромагнитный момент становился равным моменту сил сопротивления на валу АД и двигатель выходил бы на установившийся режим работы. На векторной диаграмме рис. 6.35, б вектор /, по мере увеличения нагрузки скользит по линии 1, перпендикулярной вектору Ч?2. Результирующая составляющая токов статора и ротора по оси у создает составляющую потокосцепления ЧУМГ При этом конец вектора Ч? скользит по прямой 2, также перпендикулярной вектору Ч?2- Таким образом, при увеличении нагрузки двигателя и стабилизации Ф2 поток намагничивания машины также увеличивается, что необходимо учитывать при реализации системы управления приводом со стабилизацией потокосцепления ротора. Особенностью систем управления с опорным вектором потокосцепления 4х 2 является более простая, чем при опорном векторе Ч, структура управления. В соответствии с рис. 6.35, б она должна иметь два канала управления - потокосцеплением у¥2 и скоростью двигателя. Канал управления Ч*2 двухконтурный: внутренний контур управляет составляющей 1и тока статора, внешний - модулем потокосцепления ротора. Двухконтурным может быть и канал управления скоростью АД: внутренний контур управляет составляющей 1[у тока статора, внешний - угловой скоростью ротора. Недостаток систем с опорным вектором потокосцепления ротора в том, что определение этого вектора возможно лишь расчетным путем на основе параметров АД, как правило, известных не точно и изменяющихся при работе двигателя. При стабилизации потокосцепления ротора (у¥2 = const) механические характеристики АД подобны характеристикам ДПТ с независимым возбуждением. Поскольку теория и технические решения замкнутых систем управления электроприводом с ДПТ, имеющим независимое возбуждение, достаточно апробированы, то понятна привлекательность применения систем векторного управления с управлением по потоку ротора. Структурная схема АД при управлении по вектору потокосцепления ротора. Динамические свойства короткозамкнутого АД при питании от источника напряжения в системе координат х, у при ориентации вектора потокосцепления ротора по оси х определяются следующими выражениями [8]: dt dt d*¥ #1, =-7 +VM+eWFi* (6.44) для статорной цепи и dV2x О = I2yR2 + (со0эл - рп<а)Ч>2х = I2yR2 + s 2х (6.45) для цепи ротора АД. Здесь Ulx, Uly - проекции вектора напряжения питания статора АД. Проекции векторов потокосцеплений статора и ротора на оси х, у: 4>lx=LlIlx+LuI2x; Ч>1у=ЦГ:у+Ц212у; (6.46) V2x=L2r2x+LnIlx; Ч2у=0 = Ь212у + Ц211у. (6.47) Поскольку при ориентации вектора потокосцепления ротора по оси х в системе управления АД представляет интерес определение зависимостей между переменными Ч/2 и /„ исключим из уравнений (6.44)-(6.47) переменные Ч1х, У[у, Г2х и Г2у. Из (6.47) токи ротора Ъ-О-ад,); yjrhy(6-48) l2l2 С учетом (6.48) уравнения (6.46) преобразуются к виду 4>1х = к2Ч2х +аЦ11х; 4V = аЦ11у,(6.49) где к2 - коэффициент электромагнитной связи ротора, к2 = Ll2/L2, а - коэффициент рассеяния магнитного поля АД, а = 1 - -~-. Подставив (6.49) в (6.44), для статорной цепи АД получим Ulx = к2+ al, + Т\Л ~ аЬАуЩъ*; dtdt(6.50) dl\ ~dt Уравнения (6.45) для роторной цепи с учетом (6.48) преобразуются к виду 4,,-,, (3n-Pn2X=k2R2hy (6-51) dtL2 С учетом (6.51) уравнения (6.50) примут вид dhx. Uly = аЦ + TlyRi + (к22х + а1,/и)со0эл.
dr(6-52) + аА/1хСо0эл = o-L, + /„(Я, + km + (к2Ч>2хщэл - -к22а0эл + k2pnoW2x) + aLJ]xa03Jl = к2рп(й2х + dhv + аЦ11хщэл + (Rx + klR2)Ih. +°Li-jf- Если представить в осях х, у составляющие ЭДС, наводимые в статоре, как R Е\х =к2-*¥2х +ctZ1/1>,cuo3ji; (6.53) Е\у = k2pntc№2x + аЦ11х(£>0эл, где выражение /c2-j-y¥2x = (к2Г2х + k2Ilx)R определяет падение на-Ц. пряжения в роторной цепи АД, выражения оЬ{1[ущэя и <зЬх1Ххщэп характеризуют ЭДС самоиндукции или падение напряжения на индуктивном сопротивлении цепи статора, а к2рпк2х учитывает составляющую ЭДС вращения, наводимую в статоре потокосцеп-лением ротора, то уравнения (6.52) примут вид UXx = -Е1х + (Rx + кЩ)1Хх dt Uly = Ely + (*,+ к2)11у+иЦ или в операторной форме U\x (Р) + Е]х (р) = Rb 0 + Т1эр)11х (р); Uiy(p) - Ely(p) = Л1э(1 + ТъР)11у(р), (6.54) (6.55) где Rl3 - эквивалентное активное сопротивление цепи статора, Rl3 = Rl + k2R2; ГЭ - электромагнитная постоянная времени этой цепи, 7,3 = аЬх/кХэ. Для цепи ротора уравнения (6.51) в операторной форме будут иметь вид (1 + Т2р) (6.56) [и>0м(Р)- PMP)Wlx(j>) = г!\у(Р), где Т2 - электромагнитная постоянная времени цепи ротора, Т2 = = L2/R2. В соответствии с выражением (6.42) электромагнитный момент АД при ориентации Ч/2 по оси х в операторной форме определится так: 3 V С учетом уравнения движения электропривода M(p)-Mc(p) = Jpa>(p). Структурная схема АД, соответствующая уравнениям (6.53) (6.56), представлена на рис. 6.36. Для наглядности цепи статора (С), ротора (Р) и узла, связанного с формированием ЭДС (Э), выделены штриховыми контурами. Входными переменными статорной цепи являются потокосцепление ротора Ч2х = ЧУ2, составляющие U]x, Uu, напряжения питания статора, текущая угловая скорость АД со и синхронная скорость электромагнитного поля со0эл, а выходными - составля- M{p) = -pnki2x(P)hyiP)-(6.57) 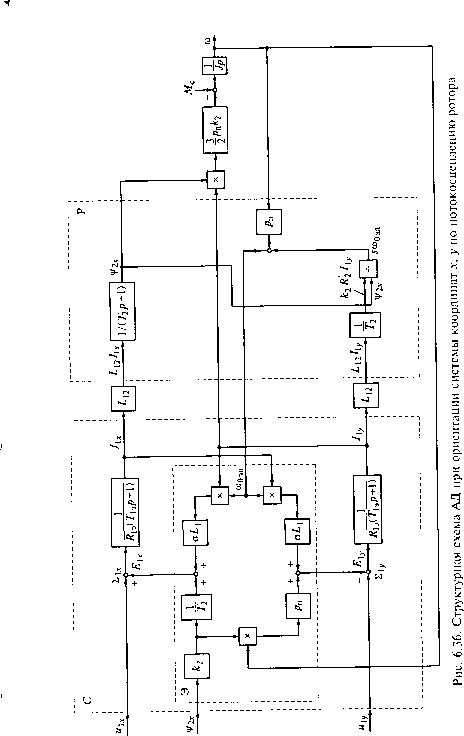 0 ... 31 32 33 34 35 36 37 ... 49 |












